相机成像线性模型

做项目时用到了有关相机内参和外参矩阵的相关知识，所以需要自己了解一些相关的基础。而涉及到相机内参和外参矩阵的内容，经查询后发现此部分跟相机标定有关。

相机标定的主要步骤就是构造一个以图像信息为输入，图像中相关物体轮廓的三维坐标集合的数学模型，然后求解该模型的未知参数（内参矩阵,外参矩阵,畸变参数）,最后应用于实际情况。

这里我们仅讨论相机的线性模型的建立,即针孔模型，不考虑畸变等复杂情况。

坐标系简介

为了更清楚的描述模型的建立的过程，这里通常会以下面四个坐标系为基础进行建模。

二维图像坐标系

二维图像坐标系其实也就是以数字图像为基础构造的坐标系，如最常见的二维数组结构组织形式。这里设定列的增长方向为u轴,行的增长方向为v轴。所以$(u,v)$表示数字图像上的某一点的像素坐标。($u,v$通常为非负整数)

二维成像平面坐标系

表示图像物理位置的坐标系，在图像坐标系的基础上乘以每像素的物理尺寸，然后再加上原点的偏移量即可。其坐标系坐标点表示为$(x,y)$

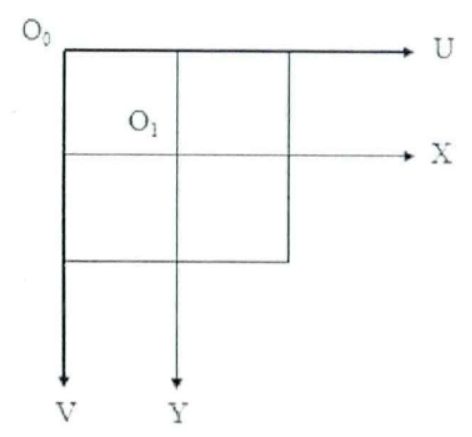
图像坐标系与成像平面坐标系之间的转换关系如下所示:

$$\left[\begin{array}{l}u \\ v \\ 1\end{array}\right]=\left[\begin{array}{ccc}1 / d x & 0 & u_{0} \\ 0 & 1 / d y & v_{0} \\ 0 & 0 & 1\end{array}\right]\left[\begin{array}{l}x \\ y \\ 1\end{array}\right]$$

其中$u_0,v_0$表示原点分别在列方向，行方向的偏移量。如果按上面图片中的理想状态，则满足$u_0=\frac{w}{2},v_0=\frac{h}{2}$。其中$w,h$为图像的宽，高。

$d_x,d_y$分别为x,y方向上每像素的物理尺寸。

三维相机坐标系

其坐标系中的点表示为$(x_c,y_c,z_c)$,其中深度$Z_c$为相机原点距世界坐标系下实物原点的距离。

成像平面坐标系与相机坐标系之间的转换关系推导:

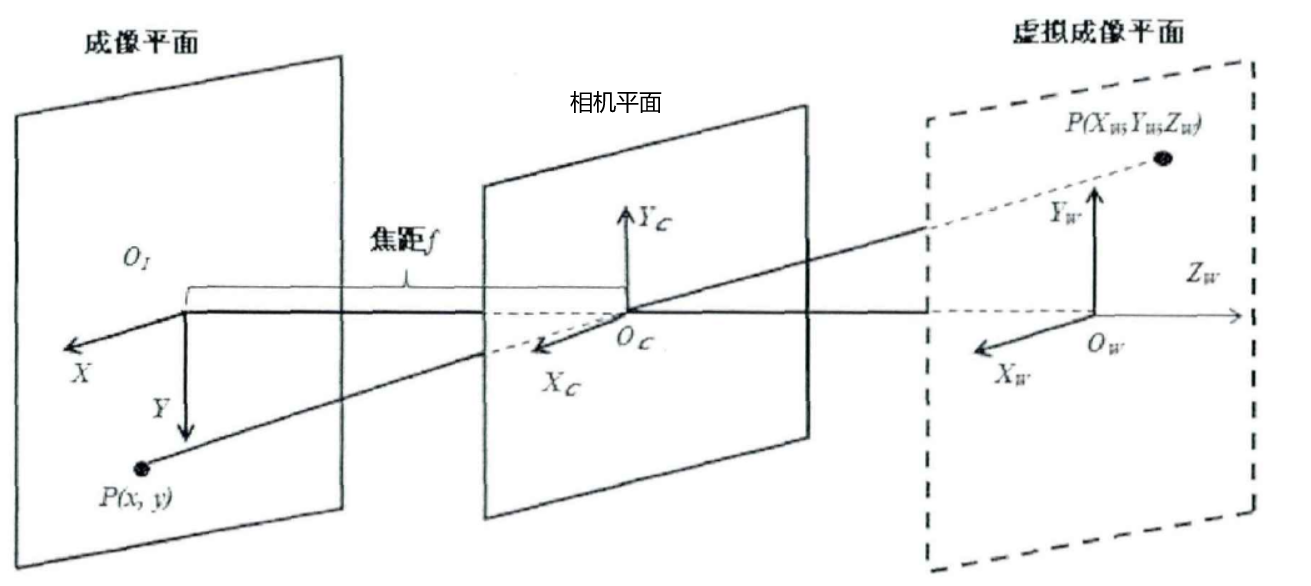
根据上图，我们可以得到如下关系:

$$\left\{\begin{array}{l}x=f \frac{x_{c}}{z_{c}} \\ y=f \frac{y_{c}}{z_{c}}\end{array}\right.$$

可以得到投影矩阵(即成像平面与相机坐标系之间的坐标的关系):

$$z_{c}\left[\begin{array}{l}x \\ y \\ 1\end{array}\right]=\left[\begin{array}{lll}f & 0 & 0 \\ 0 & f & 0 \\ 0 & 0 & 1 \end{array}\right]\left[\begin{array}{c}x_{c} \\ y_{c} \\ z_{c} \end{array}\right]$$

三维世界坐标系

用来描述物体和物体(相机)之间的相对位置关系。定义其坐标系为$(O-X_WY_WZ_W)$,其坐标系下的坐标点为$(x_w,y_w,z_w)$

世界坐标系与相机坐标系之间的坐标的关系如下所示:

$$\left[\begin{array}{c}X_{C} \\ Y_{C} \\ Z_{C} \\ 1\end{array}\right]=\left[\begin{array}{cc}R & t \\ 0^{T} & 1\end{array}\right]\left[\begin{array}{c}X_{W} \\ Y_{W} \\ Z_{W} \\ 1\end{array}\right]$$

其中$\left[\begin{array}{cc}R & t \ 0^{T} & 1\end{array}\right]$可以简单表示为$M$(外参矩阵),$t=(t_1,t_2,t_3)^T是平移矩阵$，$R$是$3\times 3$的正交单位矩阵。

图像坐标系于世界坐标系之间的转换关系

根据上面各个坐标系之间的转换，我们可以得到图像坐标系与世界坐标系之间的转换关系。

$$\begin{aligned} \left[\begin{array}{l}u \\ v \\ 1\end{array}\right] &= \left[\begin{array}{ccc}1 / d x & 0 & u_{0} \\ 0 & 1 / d y & v_{0} \\ 0 & 0 & 1\end{array}\right]\left[\begin{array}{l}x \\ y \\ 1\end{array}\right] \\ &= \frac{1}{z_{c}} \left[\begin{array}{ccc}1 / d x & 0 & u_{0} \\ 0 & 1 / d y & v_{0} \\ 0 & 0 & 1\end{array}\right]\left[\begin{array}{lll}f & 0 & 0 \\ 0 & f & 0 \\ 0 & 0 & 1 \end{array}\right]\left[\begin{array}{c}x_{c} \\ y_{c} \\ z_{c} \end{array}\right] \\ &=\frac{1}{z_{c}} \left[\begin{array}{ccc}1 / d x & 0 & u_{0} \\ 0 & 1 / d y & v_{0} \\ 0 & 0 & 1\end{array}\right]\left[\begin{array}{lll}f & 0 & 0 \\ 0 & f & 0 \\ 0 & 0 & 1 \end{array}\right]\left[\begin{array}{cc}R & t \end{array}\right]\left[\begin{array}{c}x_{w} \\ y_{w} \\ z_{w}\end{array}\right] \\ &=\frac{1}{z_{c}} \left[\begin{array}{ccc}f / d x & 0 & u_{0} \\ 0 & f_ / d y & v_{0} \\ 0 & 0 & 1\end{array}\right]\left[\begin{array}{cc}R & t \end{array}\right]\left[\begin{array}{c}x_{w} \\ y_{w} \\ z_{w}\end{array}\right] \\ &=\frac{1}{z_{c}} A M\left[\begin{array}{c}x_{w} \\ y_{w} \\ z_{w}\end{array}\right] \end{aligned}$$

其中A为相机内参矩阵，M称为相机外参矩阵

参考文献

[1] 舒娜. 摄像机标定方法的研究[D].南京理工大学,2014.